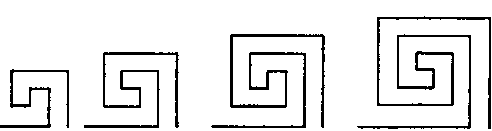
Рис. 3.29. Иерархия мотивов для меандров
3.5.7. Реализация полиспирали Напишите подпрограмму polyspiral (float length, float angle, float incr, int num), рисующую полиспираль, состоящую из num отрезков, первый из которых имеет длину length. После рисования каждого из отрезков length увеличивается на incr, а черепаха поворачивается на угол angle.
3.5.8. Является ли полиспираль IFS?
Можно ли описать спираль в категориях IFS (iterated function system - система итерируемых функций), введенных в главе 2? Задайте функцию, итерируемую черепахой на каждой итерации.
3.5.9. Рекурсивная форма для polyspiral()
Перепишите подпрограмму polyspiral О в рекурсивной форме, так чтобы polyspiral О с аргументом dist вызывала polyspiral О с аргументом dist+inc. Включите в программу подходящий критерий остановки.
1 Происходит от слова Маеапс1ег (в современном звучании Мепскгев - Мендерес), извилистой реки в Турции.
3.6. Фигуры на основе правильных многоугольников
3.6. Фигуры на основе правильных многоугольников Обобщать - значит быть идиотом.
Уильям Блейк Пчелы… в силу своей геометрической предусмотрительности… знают, что шестиугольник больше, чем квадрат или треугольник, и в нем поместится больше меда при равном расходе материала.
Паппус из Александрии (Pappus of Alexandria)
Правильные многоугольники (полигоны) составляют обширное и важное семейство форм, часто встречающееся в компьютерной графике. Нам нужны эффективные методы для их рисования. В этом разделе мы выясним, как это делать и как создавать различные фигуры, являющиеся вариациями правильного многоугольника.
3.6.1. Правильные многоугольники Вначале дадим определение правильного многоугольника.
Определение. Многоугольник называется правильным, если он является простым, если все его стороны имеют равную длину и если его смежные стороны образуют равные внутренние углы.
Как уже обсуждалось в главе 1, многоугольник является простым (simple), если никакие две его стороны не пересекаются (точнее, только смежные стороны могут соприкасаться и только в их общей концевой точке). Назовем я-угольником правильный многоугольник, имеющий п сторон. Типичными примерами я-угольников являются 4-угольник (квадрат), 5-угольник (правильный пятиугольник, или Пентагон), 8-угольник (правильный восьмиугольник, или октагон) и т. д. 3-угольник это то же самое, что равносторонний треугольник. На рис. 3.30 приведены различные примеры. Если число сторон и-угольника велико, то этот многоугольник по внешнему виду стремится к окружности. Фактически позже мы это применим как один из способов реализации рисования окружности.