Аналогичная ситуация имеет место для аквариума на рис. 14.58, б. Луч 1 вначале соударяется с аквариумом в момент наименьший из моментов времени, в которые он находится в 5,, но ни в 52, ни в С. С другой стороны, луч 2 впервые соударяется с аквариумом в момент £5. Опять же, это наименьшее значение времени, для которого луч находится в 5,, но ни в другой сфере, ни в конусе. Соударения в более ранние моменты времени являются соударениями с компонентами аквариума, однако не с самим аквариумом.

14.12. Составные объекты: логические операции с объектами

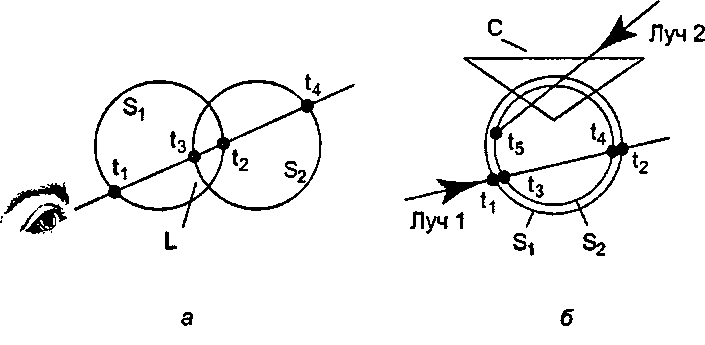
Рис. 14.58. Трассировка лучей для линзы и аквариума Сведем эти идеи в алгоритм трассировки лучей для любого составного объекта [Roth, 177]. Рассмотрим два объекта Ли В совместно с лучом. Построим список моментов времени, в которые данный луч входит в объект Л и выходит из него, и упорядочим этот список по возрастанию моментов. Поскольку объект трехмерный, моменты входа и выхода различны. Построим аналогичный список времени входа и выхода для объекта В. Оба эти списка приведены на рис. 14.59. Более темным цветом на рисунке показан каждый интервал времени между входом и выходом"images/tmp8E4A-958.png" alt="Списки значений I взаимодействия луча с двумя объектами">

Рис. 14.59. Списки значений I взаимодействия луча с двумя объектами Располагая внутренними множествами для луча с объектами АиВ, найдем внутреннее множество для этого же луча с составным объектом, построенным из Л и В. При помощи операций АиВ, АпВ, А-В, В-А можно образовать четыре новых объекта. Рассмотрим ЛиБ. Луч находится внутри объединения объектов, если он находится внутри хотя бы одного из них. Поэтому внутреннее множество для объекта ЛиБ является просто объединением индивидуальных внутренних множеств. Те же соображения применимы и к остальным трем объектам"opengl1_1016.html">⇐ Предыдущая| |Следующая ⇒