Практические упражнения
14.11.1. Эффекты, связанные с преломлением На рис. 14.51, а изображен глаз на высоте Н, смотрящий из воздуха на пруд с водой. Рыбка находится на расстоянии L от глаза по горизонтали и на глубине D. В каком месте глаз видит рыбку, если свет в воздухе распространяется вдвое быстрее, чем в воде?
14.11.2. Создание радуги На рис. 14.51, б показан луч белого света, входящий в призму с внутренним углом 60°. Призма изготовлена из плавленого кварца. Вычислите и нарисуйте траектории красного, зеленого и синего компонентов света при их прохождении внутри призмы и при выходе из нее. Будет ли видна радуга

14.11. Отражения и прозрачность
при выходе луча, если белый луч пропускается через пластину из плавленого кварца с параллельными стенками?
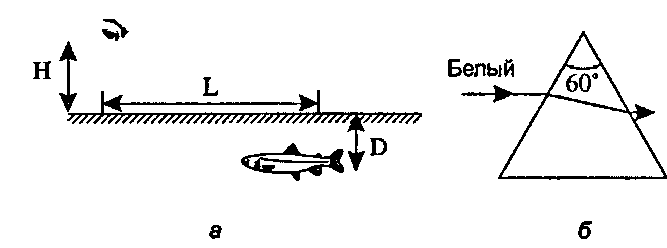
Рис. 14.51. Некоторые эксперименты с преломлением 14.11.3. Вывод направления преломленного луча На рис. 14.52 предлагается разумный способ вывода направления t преломленного луча света, который также пригодится для создания эффективного алгоритма (предложено Хекбертом [Heckbert, 104]). Единичные векторы dir и m определяют плоскость, в которой лежат как отраженный, так и преломленный лучи. На рисунке показан также единичный круг, нарисованный в этой плоскости. Поскольку все векторы единичные, длины их различных компонентов вдоль вектора m и перпендикулярно к нему численно совпадают с синусами и косинусами углов 9, и 92.
О Покажите, что вектор, обозначенный на рисунке буквой п, равен
n - cos(9,) m + dir,что его длина равна sin(9,), так что нормированный вектор ия = n/sin(9,). Докажите при помощи скалярных произведений, что вектор п лежит в плоскости векторов m и dir и перпендикулярен вектору т. О Докажите, что
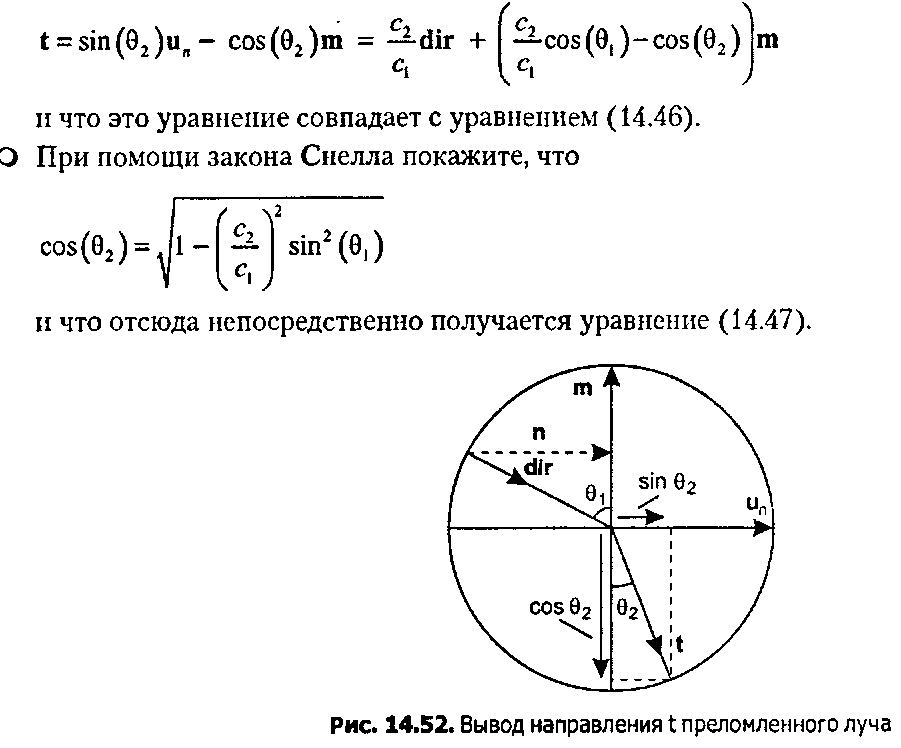
Введение в трассировку лучей
14.11.4. Подпрограмма для вычисления направления преломленного луча Напишите подпрограмму
Vector3transmitDirection(vector3 m, Vector3 dir, float cl, float c2)которая вычисляет направление вектора t по заданным единичным нормальным векторам m и dir и скоростям света в двух средах.
